AiPE
부동 소수점 방식의 정의와 컴퓨터가 부동 소수점 방식을 취하는 이유 본문
가장 먼저 나는 부동 소수점 방식에 대해 공부하면서 아래 자료를 굉장히 많이 참조했다.
https://steemit.com/kr/@modolee/floating-point
부동 소수점(Floating Point)란 무엇인가? — Steemit
안녕하세요. 개발자 모도리입니다. 이번에는 잠시 다른 주제를 다뤄 보겠습니다. (EOS Dapp 개발 공부를 못하고 있습니다.) 부동 소수점이란 무엇인가 알아보도록 하겠습니다. 이 주제 선택한 이유
steemit.com
컴퓨터가 소수점을 표현하는 방식에는 크게 "고정 소수점 방식"과 "부동 소수점 방식"이 존재한다.
부동 소수점 방식을 이해하기 위해서는
| ① 이진수 표현법 ② 고정 소수점 방식 |
위 두 가지에 대한 기초 지식이 필요하므로 이에 대해 먼저 다루어 보려고 한다.
1. 이진수 표현법과 비트
우리가 평소에 사용하는 정수 체계는 10이 되면 올림(Carry)를 진행하는 십진수(10진수)이다.
이와 달리, 이진수(2진수)는 0과 1만으로 모든 데이터와 숫자를 표현하는 방법이다.
컴퓨터는 전류가 흐르는 상태인 1, 전류가 흐르지 않는 상태인 0의 두 상태만을 처리할 수 있기 때문에
모든 컴퓨터 연산에는 이진수가 사용된다.
비트(bit)는 이진수로 표현된 숫자 하나를 의미한다.
예를 들어, 십진수 13을 이진수로 나타내면 아래와 같다.
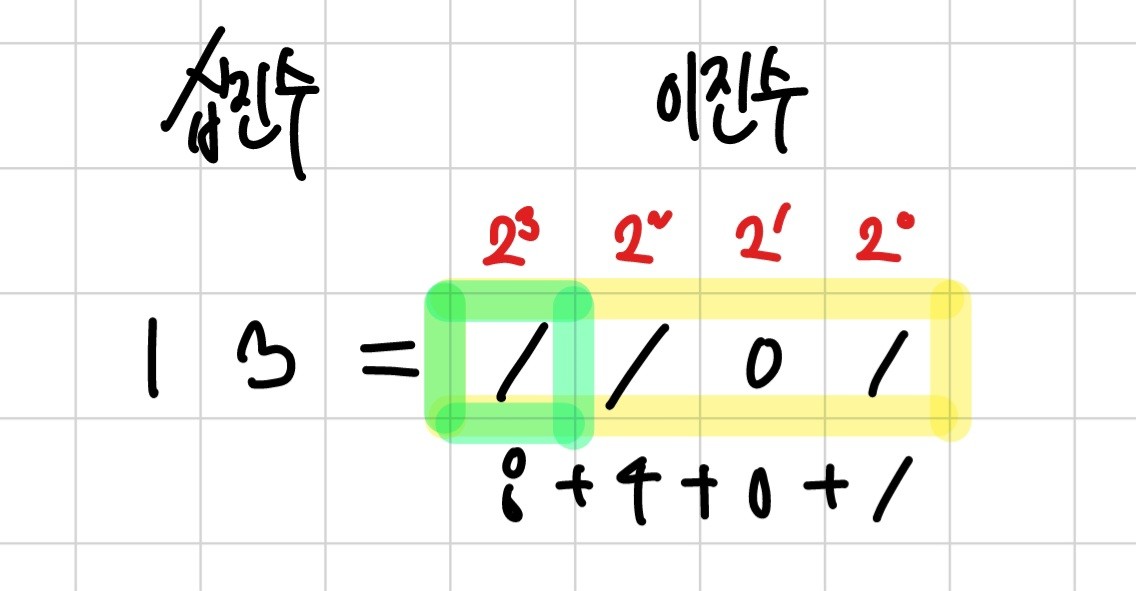
연두색 박스 하나가 1비트(bit)에 해당한다.
노란색 박스 하나가 반(0.5) 바이트(=4비트)에 해당한다.
노란색 박스 두 개가 모여야 1 바이트(byte)이다.
또한, 십진수 13은 13(10)과 같이 나타내며,
이진수 13은 13(2) 혹은 1101(2)라고 나타낸다.
위 그림에서 볼 수 있듯이, 가장 오른쪽의 비트를 기준으로 2^0, 2^1 .., 2^n 이 순차적으로 부여되며
이를 십진수로 환산하기 위해서는 각 비트에 해당하는 2^n을 모두 합하면 된다.
위와 같은 간단한 수는 쉽게 이진수로 나타낼 수 있지만, 소수점이 있는 경우 표기의 난이도가 올라간다.
예를 들어, 0.3을 2진수로 표현하면
| 0.01001100110011......(0011)의 무한 반복 |
이 된다.
cf. 소수점 아래 이진수가 들어가는 경우,
정수일 때와 마찬가지로 소수점 아래 첫 번째 자리부터 순차적으로 2^(-1), 2^(-2), ... ,2^(-n)을 의미한다.
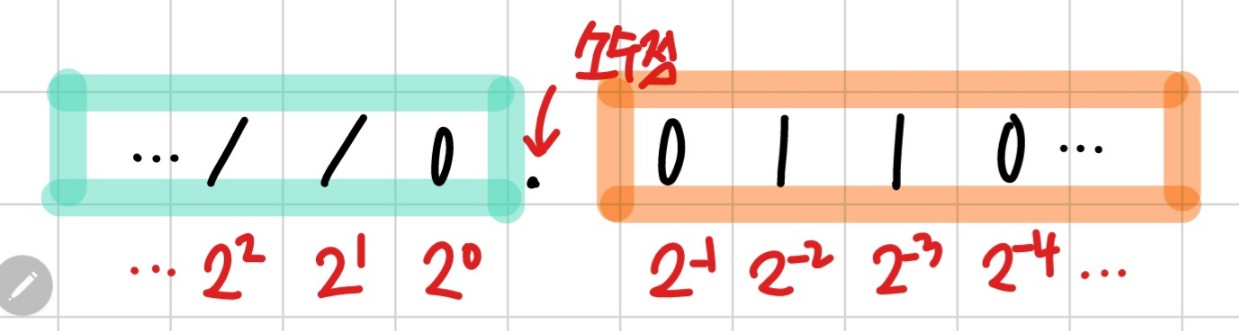 |
이렇게 무한히 순환하는 수나 원주율(π)등은 그 자릿수가 무한하기 때문에 한정된 비트를 가지고 정확하게 표현할 수 없다.
따라서 어쩔 수 없이 컴퓨터에서는 정해진 비트 수 내에서 표현할 수 있는 가장 근사치의 값이 저장된다.
이 근사 값을 저장하는 방법이 바로 고정 소수점 방식과 부동 소수점 방식이다.
2. 고정 소수점 방식
고정 소수점 방식은 정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해두고 해당 비트만큼만을 사용해 숫자를 표현하는 방식이다.
예를 들어, 정수 부분을 8비트, 소수 부분을 24비트로 표현하면, 큰 수이든 작은 수이든 표현이 가능한 수라면 정수 부분은 무조건 8비트를, 소수 부분은 무조건 24비트를 잡아먹는다.
가장 간단한 방식이지만, 아래의 3가지 큰 문제점이 발생한다.
| ① 정수를 표현하는 비트를 늘리면 큰 수를 표현할 수 있지만 소수 부분의 정밀도가 떨어진다. ② 소수를 표현하는 비트를 늘리면 작은 수를 표현하기 유리하지만 정수 부분의 정밀도가 떨어진다. ③ 정수와 소수를 표현하는 비트를 모두 늘리면 전체적인 표현의 정밀도는 올라가지만, 용량이 과도하게 커질 수 있다. |
이런 문제를 개선하기 위해 컴퓨터는 부동 소수점 방식을 고안하여 채택하고 있다.
3. 부동 소수점 방식
부동 소수점 방식은 컴퓨터에서 실수를 효율적으로 표현하기 위해 고안된 방식이다.
가장 먼저 부동 소수점 방식(floating-point representation)의 정확한 정의를 내리고 시작하자.
"부동"이라는 단어는 영어를 보아도 "둥둥 떠 다닌다"는 의미인데, 와닿지 않을 수 있으므로 이를 정확히 해보자.
| 오해하지 말아야 할 것이, 부동 소수점 방식에서의 부동이 '움직이지 않는다'의 부동이 아니다. 오히려, 둥둥 떠다닌다는 의미이므로 자유롭게 움직인다는 것이다. |
| 일반 숫자를 부동 소수점 숫자로 만드는 방법 (+ 부동 소수점 방식의 이름이 "부동" 소수점인 이유) |
| 고정 소수점 방식으로 표현된 소수를 부동 소수점 방식으로 바꾸는 과정을 보면 "둥둥 떠다닌다"는 말의 의미를 바로 알 수 있다. ① 고정 소수점 방식으로 표기된 수를 이진수로 변환한다. ex. 263.3의 경우 100000111.010011001100110...이 된다. ② 맨 앞의 한 자리정수만을 남기고 그 직전까지 소수점을 옮긴 후 자릿수를 지수로 표현한다. 소수점 앞에 있는 수를 "정수 부분"이라고 부르며, 소수점 아래의 숫자를 "부동 소수점 숫자"라고 부른다. ex. ①의 예시는 소수점을 맨 앞자리까지 당길 경우 1.00000111010011001100110... * 2^8(2의 8승) 으로 표현된다. ③ 아래 표에 따라 올바른 자리에 알맞은 수를 적는다.  - 부호 비트에는 나타내려는 수가 양수이면 0, 음수이면 1을 적는다. - 지수 비트에는 수가 a × 2^n의 꼴일 때의 n을 적는다. - 가수 비트에는 소수점 이하의 수를 가능한 만큼 적는다. Ex. 263.3은 양수이므로 부호 비트에 0을 적는다. 2^8에서 8을 2의 지수라고 하며, 하늘색 부분에 적는다. 나머지 00000111010011001100110...을 가능한 만큼 초록색 부분에 적는다. 실제 정수가 몇 자리 숫자였는지에 관계 없이 소수점을 마음대로 옮긴 후, 지수로 컨트롤했으므로 소수점이 둥둥 떠다닌다는 것이 어떤 의미인지 이해할 수 있다. |
위 표는 <IEEE 754 표준>이라는 표이다.
부동 소수점 방식은 <IEEE 754 표준>이라는 것에 의거해 정의되어 있다.
Java SE와 비슷하게, 부동 소수점을 어떻게 표현하며 연산해야 하는지에 대해 규정한 표준안이다.
https://ko.wikipedia.org/wiki/IEEE_754
IEEE 754 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. IEEE 754는 IEEE에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준이다. ±0 등의 수와 무한, NaN 등의 기호를 표시하는 법과 이러한 수에 대한
ko.wikipedia.org
4. 컴퓨터가 부동 소수점 방식을 채택하는 이유
부동 소수점 방식을 채택하는 이유는 다음과 같다.
| 부동 소수점 방식을 채택하는 이유 (=장점) |
| ① 범용성과 효율성 부동 소수점 방식을 통해 다양한 범위와 정밀도를 가지는 실수를 표현할 수 있다. 매우 큰 수, 매우 작은 수 모두를 동일한 방식으로 표현할 수 있다. ② 표준화에 따른 이식성과 호환성 국제적으로 모든 언어가 사용하는 표준안을 따르기 때문에 이식성과 호환성이 비약적으로 상승한다. 서로 다른 시스템간 실수를 표현하고 계산할 때 효율적이다. |
5. 부동 소수점 방식의 단점
이러한 부동 소수점 방식에도 필연적인 단점이 존재한다.
| 부동 소수점 방식의 단점 |
| ① 정밀도 손실 후술할 원리를 살펴보면 알겠지만, 부동 소수점 방식은 정밀도가 어느정도 한정되어 있다. 따라서 매우 작은 수나 매우 큰 수를 정밀하게 표현하기 부적합할 수 있다. ② 반올림 오차 소수점 연산 등에서 반올림 오차가 발생할 수 있으며, 계산 결과에도 약간의 오차가 발생할 수 있다. |
이러한 오차 때문에 정밀한 과학 실험이나 금융 분야 등 정확한 숫자 표현과 연산이 필요한 경우 부동 소수점 방식을 적용하기에 부적합할 수 있다.
'[XiBBaL] Study > Java' 카테고리의 다른 글
| 컴파일러(Compiler)와 인터프리터(Interpreter)의 정의와 장단점 및 특징 (0) | 2024.03.25 |
|---|---|
| Java 자료형 총정리 (0) | 2024.03.25 |
| 보수(Complement)의 정의와 컴퓨터가 음수를 보수로 저장하는 이유 (0) | 2024.03.25 |
| Java의 반복문 문법 (0) | 2024.03.25 |
| Java SE / JDK / JRE / JVM 용어 정리 (0) | 2024.03.25 |

